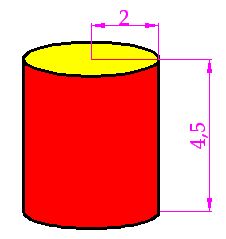
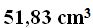VOLUMEN DE UN CILINDRO
Según lo que acabamos de decir, el volumen de un cilindro lo hacemos del mismo modo como si fuésemos a calcular el de un prisma: 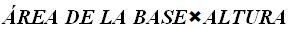
Respuesta:
Solución:
Construir un cilindro:
Sirviéndote de regla, compás, cartulina, tijeras y pegamento, dibujas una plantilla parecida a la que tienes a continuación, la recortas, doblas y aplicas el pegamento en las solapas:
Sirviéndote de regla, compás, cartulina, tijeras y pegamento, dibujas una plantilla parecida a la que tienes a continuación, la recortas, doblas y aplicas el pegamento en las solapas:
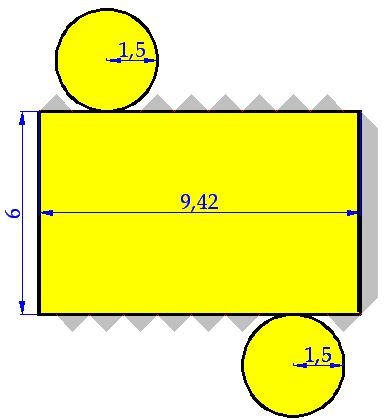
Las solapas en forma de triángulos es mejor para pegar superficies curvas.
La longitud de la cartulina rectangular ha de coincidir con la longitud de la circunferencia de la base 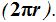
15(3).33 Un depósito de forma cilíndrica tiene como radio de las bases 3 m. La altura del depósito es de 4 metros. ¿Cuántos litros de agua puede contener?.
Respuesta: 113.097,336 litros
Solución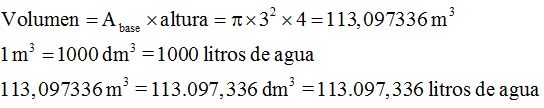
CONO
Palabra procedente del griego konos = piña, punta.
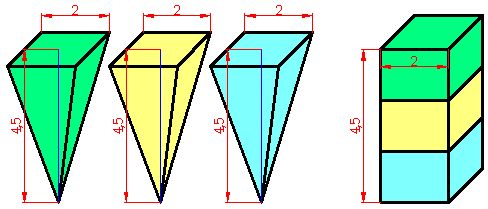
Recordamos en primer lugar a la pirámide regular. Sus caras laterales son triángulos isósceles y la base, un polígono regular. La altura es la perpendicular que partiendo del vértice llega a la base y su volumen equivale a:
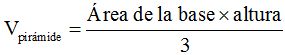
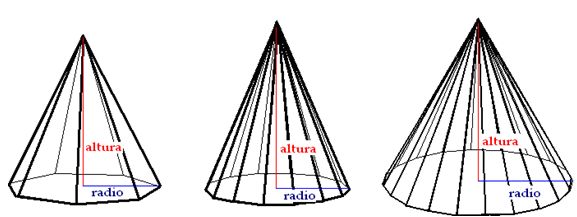
En la última figura tienes una pirámide regular cuyo polígono de la base es un heptágono (7 lados), a continuación una pirámide tetragonal porque su base es un tetradecágono. La tercera pirámide tiene como base un polígono de 20 lados o icoságono.
Analizando las tres figuras observamos que cuanto más lados tiene el polígono de la base más se parece a un cono.
Podríamos decir que un polígono de muchos lados se parece a un círculo y el área de la base será Analizando las tres figuras observamos que cuanto más lados tiene el polígono de la base más se parece a un cono.
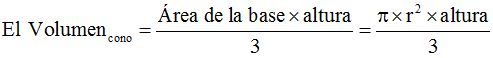
Construcción del cono
Con los utensilios habituales dibujamos la plantilla siguiente: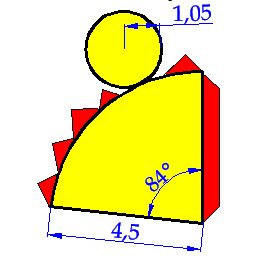

15(3).34 Calcula el volumen del cono que tienes en la figura siguiente cuyas medidas en centímetros aparecen en la misma:
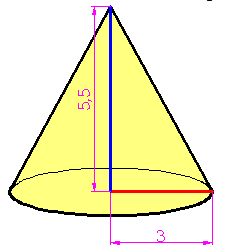
Respuesta: